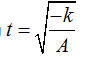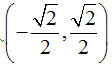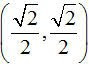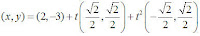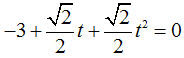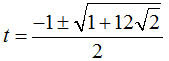Almost every Alg II class in America (
and most geometry classes) contains problems such as "Write the equation of a circle with a radius of 5 and a center at (3,1)." The assumption is that the circle lies in the x-y plane.
I stood in an Alg II classroom recently as students worked through a worksheet of such problems and wondered how hard it would be to extend this idea to write the equation of a circle with a given radius and center in ANY plane. The response is that it should be amazingly easy if we are familiar with the simpler ideas of using vectors.
The first step would be to develop the vector equivalent of the standard circle
equation, something like (x,y) = (h, k) + r cos(t) (1,0) + r sin(t) (0,1) where t has a domain from 0 to 2 Pi (or the equivalent in degrees). Then in any other plane, all that would be needed would be to replace the two unit vectors in the x and y direction with two perpendicular unit vectors in the desired plane.
Since each of the desired vectors would be perpendicular to each other and the normal to the plane we could pick one arbitrarily, then find the second using the cross product of the first with the normal to the plane.
Here is an example: " Find the circle with radius 5 and center at (3,1,2) in the plane x + y + 2z = 8. " Any vector perpendicular to (1,1,2) will work for the first direction vector, so (2,0,-1) is an easy choice. The cross product of (1,1,2) and (2,0,-1) will then be perpendicular to (2,0,-1) and lie in the desired plane. The cross product gives (1,-5, 2) for the perpendicular direction vector. Now we just write the equation using unit vectors in the directions of (2,0,-1) and (1,-5, 2). The equation for the circle requested is (x,y,z) = (3,1,2) + 5 cos(t) (2,0,-1)/sqrt(5) + 5 sin(t) (1,-5,2)/sqrt(30).
Checking that a given value of t meets all the requested, I pick pi/6 as an easy
choice. The point will be (x,y,z) = (3,1,2) + 5 sqrt(3)/2(2,0,-1)/sqrt(5) + (5/2)(1,-5,2)/sqrt(30). So x=7.3294 (appx) and y=-1.2822 and z= 0.9764.
If we are close this point should lie in the correct plane, and also be five units from the center, (3,1,2).
One more thing that starts to happen when you use vectors and write an equation in the x-y plane, such as a circle, is that you begin to imagine pulling it out in the z-direction. If you do this as a function of t, then you create a helix that coils around the z-axis as it climbs. A unit circle climbing at a rate of t/pi will climb one unit up the z-axis for each half turn of the circle. Using the equations x,y,z= cos(t)(1,0,0) + sin(t) (0,1,0) + t/pi (0,0,1) is an example.
Other conics: It is simple to extend the circle to an ellipse by just replacing the radius in the appropriate places with the semi-major/minor axis lengths, a and b. The Ellipse centered at (3,1) with a=5, b=4 would be (x,y) = (3, 1) + 5 cos(t) (1,0) + 4 sin(t) (0,1).
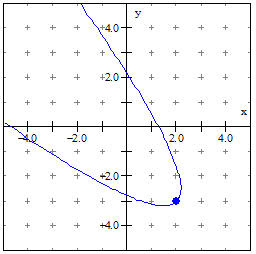
As with quadratics, it is easy to write the ellipse rotated to lie along any line through the center. For example, if we wanted to rotate the ellipse above so that it made a 45 degree angle, we simply replace the two unit vectors in the x and y direction with unit vectors [sqr(2)/2, sqr(2)/2] and [-sqr(2)/2, sqr(2)/2].
Using decimal approximations for ease of writing, the equation becomes (x,y) = (3, 1) + 5 cos(t) (.707, .707) + 4 sin(t) (-.707,.707). The Winplot graph looks like this:
For fans of Geogebra, you can download a
ggb sketch that will allow you to rotate a conic through any radian value.
For the hyperbola, simply replace the cosine and sine with tangent and secant (or secant and tangent to have the two branches open the other way).